Putting a Face to Mathematics
In less than a week H3 has had a retina scan for airport security plus a 15-point face scan for new drivers’ licences. How does this technology work and what role does Mathematics play in it?
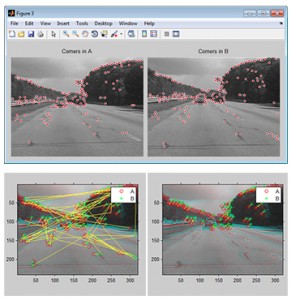
Face recognition is the process of identifying one or more people in images or videos. Algorithms for face recognition typically extract facial features and compare them to a database to find the best match. Face recognition is an important part of many biometric, security, and surveillance systems, as well as image and video indexing systems. The Mathematics behind these systems uses complex, multiple algorithms to isolate and combine features in the images. For example, this picture shows the points used in a video stabilisation system. Researchers at Cornell U make the following comment about the background math in their recognition systems:
“When one thinks of face recognition, one immediately thinks of finding features of a face: eyes, nose, ears, cheek bones. But who’s to say that these are the most distinguishing characteristics of a face, and that they are the best features by which a face should be described? And what if these features are correlated? Instead of hard-coding features for detection, we decided to find the orthogonal features that most optimally describe our large training set by using Principal Component Analysis. This creates an orthogonal basis of principal components for our training set. The basis vectors are known as eigenfaces, and can be thought of as characteristic features of a face. All new faces will be described as a linear combination of these eigenfaces. This is equivalent to projecting the new face onto the subspace spanned by our eigenfaces. By using only the eigenfaces with the highest eigenvalues, we ensure that our projection maintains the most face-like energy from the image. This method was proposed by M. Turk and A. Pentland in 1991.”
