Sound Waves and Noise Cancelling
 |
 |
| Play the note A | Play the (shifted) note A |
You may have seen advertisements for “noise reducing” headphones. Here’s a rough idea of how they work. First they figure out what kind of noise is reaching your ears. Essentially this means it figures out the sine waves of the ambient sounds. Then it creates additional noise whose sine waves cancel out the ambient sounds. It’s strange, but true: you add together the original noises and new noises, and it all just seems to disappear!
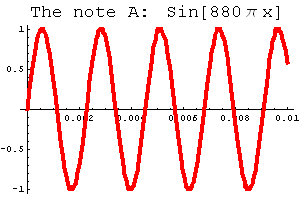
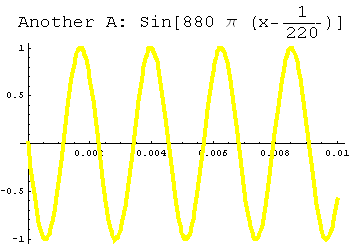
Here’s an example. Above left you’ll see the note A sound curve (in red). On the right (in yellow) is a phase shift to create another sine wave with the same amplitude and period. If you listen to the sound file, you’ll see that this also corresponds to the note A.
 |
 |
| Play this “sound” |
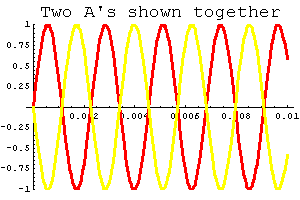
Suppose your neighbor keeps playing a recording of the original A note, and it’s driving you nuts. It turns out the shifted version above is just the thing to prevent a headache. Below you can see these two sounds graphed together; that picture should help you believe that, when you add these two sine waves together, they cancel, and you get zero. Ahhhhh, peace and quiet….Read the full article here. Also, check out James May’s excellent explanation of how noise cancelling works:
