Rogue research with Mathematics
Rogue waves (also known as freak waves, monster waves, killer waves, extreme waves, and abnormal waves) are relatively large and spontaneous surface waves that occur far out in open water, and are a threat even to large ships and ocean liners. (source: Wikipedia). Some of these waves can reach up to 10 storeys high. A recent article found on the abc network described research being done by a Physics team at the Australian Australian National University (ANU) in Canberra. “Rogue waves are more than two times the average height of the highest waves, they are unpredicted and unexpected,” research leader Nail Akhmediev said.
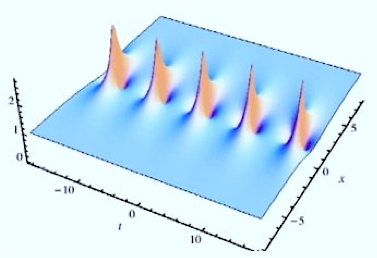Professor Akhmediev’s physics team has been explaining what rogue waves are using mathematical terms. “Data from buoys and satellites around the world is already being collected and analysed,” he said. “Combined with observations of the surrounding ocean from the ship, this would give enough information to predict rogue waves.”
In future, scientists hope equipment could be developed for ships which could predict dangerous waves in the area.The wave research has been published in the prestigious journal, The Proceedings of the Royal Society. What a great, practical application of Mathematics, especially if you like swimming or boating!
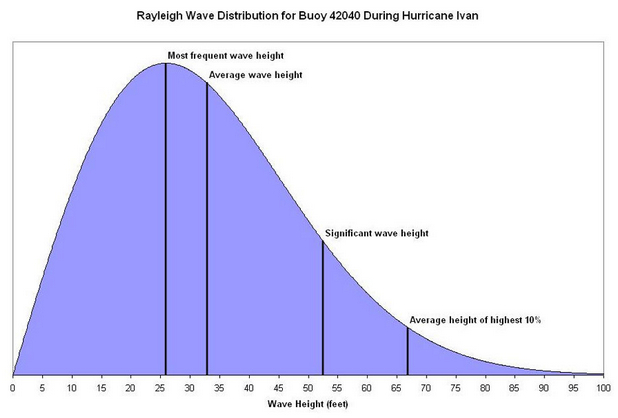
Check out Professor Akhmediev’s details and research at ANU here.
