How many 5-sided tile patterns can we make?
 Until recently, there were just 14 known convex pentagons (nonregular, five-sided shapes with outward-pointing angles) that could “tile the plane” (be arranged with flush sides on a flat surface, with no gaps or overlaps). But last month, some thirty years since the 14th was discovered, a 15th was identified.
Until recently, there were just 14 known convex pentagons (nonregular, five-sided shapes with outward-pointing angles) that could “tile the plane” (be arranged with flush sides on a flat surface, with no gaps or overlaps). But last month, some thirty years since the 14th was discovered, a 15th was identified.
The convex pentagon in question and the tiled plane that it generates appear in yellow in the bottom right square of this image:
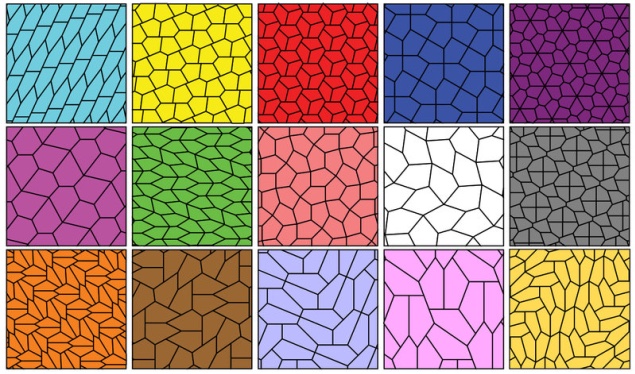 Mathematicians have proved that all triangles and quadrilaterals, or shapes with four sides, can tile the plane, and they have documented all of the convex hexagons (6 sided shapes) that can do it. But it gets a lot more complicated when dealing with pentagons — specifically convex, or nonregular pentagons with the angles pointing outward. The number of convex pentagons is infinite — and so is the number that could potentially tile the plane. It’s a problem that’s almost unsolvable because, as mathematician Jennifer McLoud-Mann (seen here) put it, it has “infinitely many possibilities.”
Mathematicians have proved that all triangles and quadrilaterals, or shapes with four sides, can tile the plane, and they have documented all of the convex hexagons (6 sided shapes) that can do it. But it gets a lot more complicated when dealing with pentagons — specifically convex, or nonregular pentagons with the angles pointing outward. The number of convex pentagons is infinite — and so is the number that could potentially tile the plane. It’s a problem that’s almost unsolvable because, as mathematician Jennifer McLoud-Mann (seen here) put it, it has “infinitely many possibilities.”
It’s a problem that also intrigued her because it was so simple that anyone could start working toward a solution using pencil and paper.
“The cool thing in mathematics is that sometimes you have a simply stated problem that doesn’t have a simple solution,” she said.
It’s possible that that there are dozens — hundreds, thousands even — of these convex pentagon shapes waiting to be discovered. Up until last month, only 14 had been found, and for all anyone knew, that list could have been final.”
Read the full article from i09 here
