In Mathematics there are numbers that are like pure gold – they glow with special properties. Like the magic ring in Lord of the Rings, they release powers of the imagination and can be used to inflict their magic on those unsuspecting students who look at them too closely. Yes, we are talking about The Golden Ratio. This is the ratio given by one side of a rectangle divided by another – in this way:
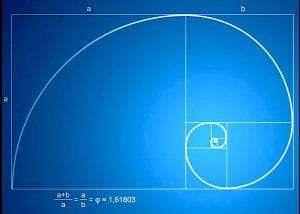Make a square with side lengths of 10cm (or 4 inches). Mark the midpoint of one side (at 5cm or 2 inches). Join this midpoint to any corner. Use a ruler to measure this line and draw it along the bottom of your square. (Or you can use that line from the midpoint as the radius to draw an arc that defines the height of the rectangle). This new length from the midpoint divided by a side of your square is called the “Golden Ratio”. It is often symbolized using phi, after the 21st letter of the Greek alphabet, and is approx. 1.168 [H3 note: use a compass to be more accurate in your construction]

Even today, the golden ratio comes handy when we have to make visually appealing web pages, brochures, or even logos for your company or a client.